Faster Sine Approximation Using Quadratic Curve
Sine waves, aptly named after the sine function which graphs them, are often used in game development. Beyond the relation to the law of sines and geometric applications – which is the first thing that comes to mind for me, sine waves are often exploited in other applications for their smooth gradients and oscillating nature and are ideal for representing a wide range of processes.
Now that we’ve established sine waves are important, the first question that comes to mind is “How much does this cost?”. Trigonometric functions such as sin() are usually considered “expensive” since they are not natively supported by most processors and require a set of atomic operations to compute.
Postponing the philosophical discussion about micro optimizations for a moment, for the time being it’s sufficient to say the question of how to optimize sine computation at the application level is not a new one. One common solution to the problem that’s been around for a while is to use a precalculated lookup table. In theory, we’d be reducing time complexity while increasing space complexity. This solution also suffers from reduced accuracy, since we can only have the outputs for a predefined set of inputs, and increasing our accuracy means adding more samples, which increases our memory requirement. There’s also hybrid solution ideas such as keeping a relatively low sample count and linearly interpolating between samples.
Reading up some more on lookup based solutions, it would seem the general consensus on the internet is that as of writing this, in most cases using a lookup table will give worse results than simply computing sine. This is attributed to the increasing gap between processor speed and memory speed, or simply put, what worked fine years ago is irrelevant in most cases today.
Going back to searching for sine optimizations, I’ve stumbled into a blog post by Michael Baczynski which suggests using a quadratic curve to approximate sine. The idea looked interesting, so I’ve decided to test it in Unity and see how it compares to Unity’s Mathf.Sin() (while discarding the suggestion to inline it by hand, we’ll leave that to the compiler, and implementing some suggestions from the comments on his post favoring addition ops to multiplications).
This is the C# version:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
// Low percision sine approximation public class SineLP { private static float sin = 0; public static float Sin( float x ) { if (x < -3.14159265f) x += 6.28318531f; else if (x > 3.14159265f) x -= 6.28318531f; if ( x < 0 ) return x * ( 1.27323954f + 0.405284735f * x ); else return x * ( 1.27323954f - 0.405284735f * x ); } } // High percision sine approximation public class SineHP { private static float sin = 0; public static float Sin( float x ) { if (x < -3.14159265f) x += 6.28318531f; else if (x > 3.14159265f) x -= 6.28318531f; if ( x < 0 ) { sin = x * ( 1.27323954f + 0.405284735f * x ); if ( sin < 0 ) sin = sin * ( -0.255f * ( sin + 1 ) + 1 ); else sin = sin * ( 0.255f * ( sin - 1 ) + 1 ); } else { sin = x * ( 1.27323954f - 0.405284735f * x ); if ( sin < 0 ) sin = sin * ( -0.255f * ( sin + 1 ) + 1 ); else sin = sin * ( 0.255f * ( sin - 1 ) + 1 ); } return sin; } } |
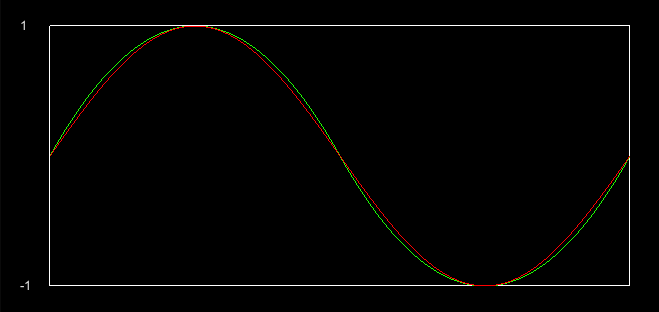
Here’s a visualization of Mathf.Sin, SineLP.Sin and SinHP.Sin with 360 samples in the range of [ 0 .. 2PI ]:
As you can see, the high precision version offers little error compared Mathf.Sin, and while the low precision version is not as accurate, it can still be used in places where the accuracy is not key factor like easing or interpolation for animation.
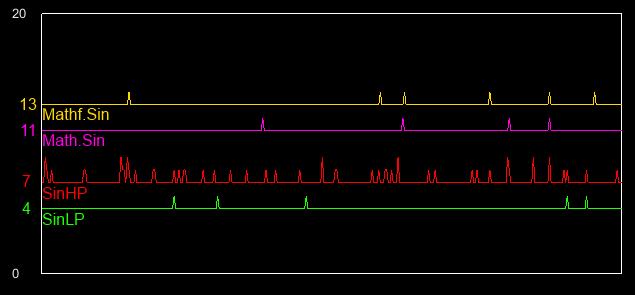
Performance wise, I’ve ran a limited benchmark test – timing the execution of each method 360,000 times per frame (1000 iterations of 360 iterations in the range of [ 0 .. 2PI ] times), over time. Here’s the results:
Conclusion?
Overall, performance wise this method looks quite promising. It’s worth benchmarking on other devices as well before pushing this into production, seeing how it compares on Atom and ARM devices.
So, should I replace all my Mathf.Sin calls with this now?
In short, no. I’ve said I’ll postpone the philosophical debate, not ignore it – and that’s just it. If there’s any decisive conclusion that can be made here is that computing sine on modern devices is pretty damn fast all around. If you find yourself computing sine thousands of times per frame, the first thing you should do is try to answer why you are doing it. That said, if you really do need to compute sine thousands of times per frame, this offers a nice solution and definitely worth keeping in mind.
Links
Wikipedia Definition for Sine Wave
Precalculated Table of Trigonometric Functions
The Gap between Processor and Memory Speeds, Carlos Carvalho
Fast and accurate sine/cosine approximation, Michael Baczynski